Flugzeuge, die wenige Dutzend Meter über die Dächer von Wohnsiedlungen donnern, Schiffsantriebe, deren Getöse Lebewesen im Meer verschreckt, Autos, deren Antrieb einen Geräuschteppich über Städte legt: Viele Verkehrsmittel verursachen Lärm, der nicht nur störend ist, sondern auch krank machen kann. Trotzdem müssen etwa die Anwohner in der Einflugschneise des neuen Berliner Großflughafens BBI zum Teil seit Jahren um die teuren Lärmschutzmaßnahmen kämpfen.
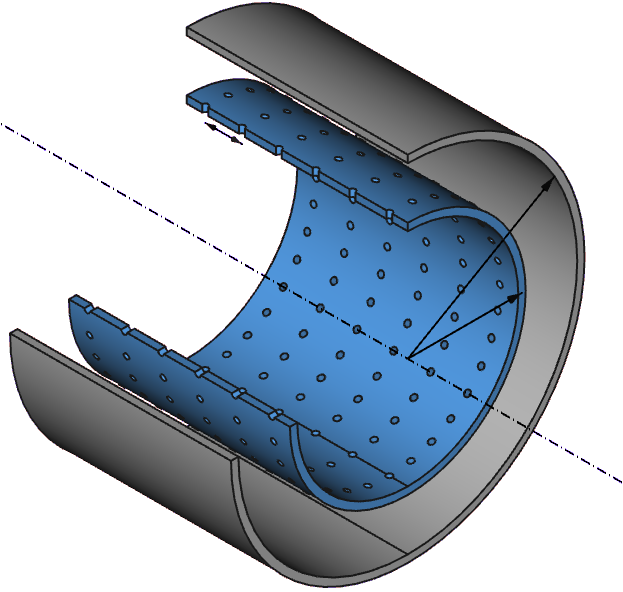
Unterdessen arbeiten ForscherInnen daran, Lärm schon an der Quelle zu reduzieren. Ein wichtiges Bauelement dafür sind perforierte Wände, wie man sie etwa aus Konzert- oder Hörsälen kennt. Die mit vielen kleinen Löchern versehenen Platten werden als Schallabsorber auch in Triebwerken von Flugzeugen oder in Schiffsantrieben und in Abgasanlagen von Autos eingesetzt.
Schalldämpfung optimieren durch Simulation
Um sie noch gezielter zum Dämpfen von Schall designen zu können, ist ein detailliertes Verständnis ihrer Wirkweise unerlässlich. Dabei interessieren vor allem die Größe und die Verteilung der Löcher, abhängig von der Frequenz des Schalls. Weil Messungen dieser Zusammenhänge unter den realen Bedingungen großer Hitze und Drücke in Triebwerken oder anderen Antrieben extrem teuer sind, sind für die Optimierung des Schallschutzes Simulationen essenziell. Direkte numerische Verfahren, wie sie bereits genutzt werden, sind allerdings sehr aufwendig und selbst auf Rechenclustern kaum realisierbar.
WissenschaftlerInnen um Dr. Kersten Schmidt vom Berliner Forschungszentrum Matheon (Einstein Zentrum für Mathematik Berlin ECMath), haben jetzt neue mathematische Modelle entwickelt, die die Simulationen erheblich vereinfachen. Sie sind dadurch wesentlich schneller und mit geringerem Rechneraufwand möglich. Von den Ergebnissen sollen künftig auch diverse Turbinenhersteller aus der Region Berlin profitieren, zum Beispiel Siemens Energy, Alstom, MTU, MAN Diesel&Turbo sowie Rolls-Royce. Erste Gespräche wurden bereits geführt.
Zu diesen Ergebnissen haben die Post-Doktoranden Dr. Adrien Semin und Dr. Anastasia Thöns-Zueva in Schmidts Team und internationale KooperationspartnerInnen beigetragen, unter anderem Dr. Bérangère Delourme von der Université Paris 13 und weitere PartnerInnen aus mathematischen und technischen Forschungsinstituten. So stellen Ingenieure für Triebwerksakustik um Dr.-Ing. Friedrich Bake vom Deutschen Zentrum für Luft- und Raumfahrt (DLR) in Berlin Messwerte aus Triebwerken zur Verfügung.
Leiser machen heißt den Schallwellen Energie entziehen
In Luft breitet sich Schall als Dichteschwankung der gasförmigen Luftmoleküle aus wie eine Welle. Dabei ist die Wellenlänge beziehungsweise deren Kehrwert, die Frequenz, das Maß für die Tonhöhe. Die Amplitude der Welle, also die Höhe der Wellenberge, bestimmt die Lautstärke.
Um sie zu reduzieren, muss der Welle Energie entzogen werden. Das passiert zum Beispiel, wenn Schall auf eine perforierte Wand trifft oder an ihr entlang geleitet wird. Zwei Mechanismen sind dafür verantwortlich, dass es leiser wird: Zum einen entsteht entlang der Wand eine dünne Grenzschicht, in der die Gasmoleküle abrupt abgebremst werden und dabei Energie verlieren. Zum anderen regen die vorbeiströmenden Gasteilchen die Luft in den Löchern ebenfalls zu Schwingungen an. Das führt zu vermehrter Reibung der Luftmoleküle untereinander und an den Wandflächen, Schallenergie wird in Wärme umgewandelt.
Neue mathematische Modelle als Grundlage für effizientere Simulationen
Als Grundlage für einfachere und effizientere Simulationen dieser Effekte entwickeln die MathematikerInnen um Dr. Kersten Schmidt neue mathematische Modelle, mit denen sie die Wechselwirkung von Schall und perforierter Wand und damit deren akustische Eigenschaften beschreiben. Ausgangspunkt dafür sind bekannte physikalische Gleichungen aus der Strömungsmechanik. Wichtig für ihre Berechnungen ist, dass die Löcher und ihr Abstand untereinander sehr viel kleiner sind als die Wellenlänge des Schalls.
Ziel der Modelle ist es, die im einzelnen sehr komplexen physikalischen Zusammenhänge durch möglichst starke Vereinfachungen zu beschreiben, ohne wesentliche Effekte zu vernachlässigen. Dafür betrachten die MathematikerInnen das Problem auf verschiedenen Größenskalen: Zunächst auf einer globalen Ebene als Wand mit vielen Löchern. Hierbei wollen sie von den Details der perforierten Struktur abstrahieren. Ein wesentlicher Trick ihres Ansatzes besteht darin, die Zahl der Löcher immer größer und ihren Abstand immer kleiner werden zu lassen. Dabei verändern sie Durchmesser und Abstand der Löcher so, dass sich die akustischen Eigenschaften kaum verändern. Im Grenzfall beschreibt das eine Wand mit unendlich vielen unendlich kleinen Löchern.
Was für den Laien besonders kompliziert erscheinen mag, erweist sich bei der mathematischen Behandlung als Vorteil: „Wir können das so einfacher beschreiben und auf Computern simulieren“, sagt Dr. Kersten Schmidt.
Um die akustischen Eigenschaften in Gänze zu erfassen, müssen die MathematikerInnen zusätzlich ein einzelnes Loch in seiner Umgebung aus unendlich vielen Löchern beschreiben. Erst im Zusammenspiel dieser beiden Perspektiven gelingt es ihnen, die akustischen Eigenschaften der perforierten Wand abzuleiten.
Dass sie mit der Qualität ihrer Modelle zufrieden sein können, zeigte der Vergleich ihrer Ergebnisse mit denen aus direkten numerischen Simulationen einer Struktur mit hunderten Löchern. „Damit haben wir gezeigt, dass unser hier beschriebener Ansatz der Oberflächenhomogenisierung effektive Eigenschaften von perforierten Wänden hervorsagen kann“, resümiert Dr. Kersten Schmidt. „In nächsten Schritten werden wir die Modelle verfeinern und weitere physikalische Aspekte berücksichtigen, zum Beispiel, dass Schall aus mehreren Frequenzen bestehen kann und wie diese Frequenzanteile sich gegenseitig beeinflussen.“
Berücksichtigung weiterer physikalischer Effekte verfeinert die Modelle
Ihr zunächst recht einfaches Modell erweitern die MathermatikerInnen nun, indem sie immer weitere Effekte betrachten. So hat Dr. Anastasia Thöns-Zueva untersucht, wie Schallwellen verschiedener Frequenzen miteinander wechselwirken, wenn sie auf die dünne Grenzschicht direkt vor der Wand treffen und abrupt abgebremst werden. Dafür hat sie ebenfalls vereinfachte und gut berechenbare Modelle entwickelt. Darauf aufbauend will sie nun das Verhalten des Schalls in den winzigen Löchern der Absorberstrukturen genauer verstehen. Denn auch dort trifft ein Frequenzgemisch auf Grenzschichten. Ihre Erkenntnisse werden dann für die Triebwerksakustiker am DLR interessant.
Auch Dr. Adrien Semin hat weitere Effekte berechenbar gemacht, die beim technischen Einsatz der Absorberstrukturen eine Rolle spielen: die Grenze zwischen einer normalen und einer perforierten Wand. Er konnte sowohl theoretisch als auch mit aufwendigen Simulationen zeigen, dass die dabei erhaltenen Modelle die Beschreibung der akustischen Eigenschaften weiter verbessern. Die Komplexität bleibt dabei so klein, dass das Problem in der Praxis berechenbar ist.
Nutzen der neuen Modelle für andere Effekte und Anwendungen
Die Ergebnisse der Matheon-MathematikerInnen und ihrer KollegInnen helfen übrigens nicht nur, den Lärm von Triebwerken zu reduzieren. Weil ganz ähnliche Phänomene auch in den Brennkammern der Triebwerke vorkommen, können perforierte Wände dort helfen, Instabilitäten beim Verbrennungsprozess so zu kontrollieren, dass sie keine mechanischen Schäden verursachen. Das verlängert die Lebensdauer.
Die neuen Ansätze sind nicht nur in der Akustik nützlich. Sie lassen sich auch auf ganz andere Anwendungen übertragen, wie zum Beispiel die Ausbreitung optischer Wellen oder die Leitung von elektrischem Strom. Auch dort werden messbare Eigenschaften wie der Widerstand durch Phänomene auf sehr kleinen Skalen beeinflusst, zum Beispiel durch Effekte an den Grenzflächen der elektrischen Leiter (Skineffekt).
Weitere Auskünfte erteilt Ihnen gern:
Dr. Kersten Schmidt
+49 (0)30 314 25 795
kersten.schmidt-aet-math.tu-berlin-punkt-de
